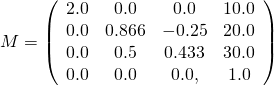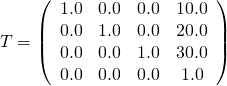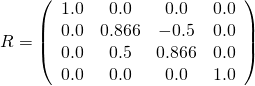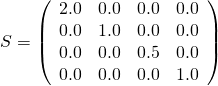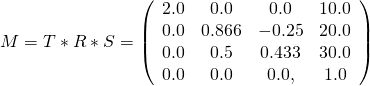【译】glTF教程:场景和节点(四)
场景和节点
场景
一个glTF文件中可能存储有多个场景,但在多数情况下,只有一个场景,即默认场景。每个场景都包含一个nodes数组,它们是场景图的根节点的索引。同样,可能存在多个根节点,形成不同的层次结构,但在多数情况下,场景只有一个根节点。在上一节中已经展示了一个尽可能简单的包含具有单个节点的单场景描述:
"scenes" : [
{
"nodes" : [ 0 ]
}
],
"nodes" : [
{
"mesh" : 0
}
],
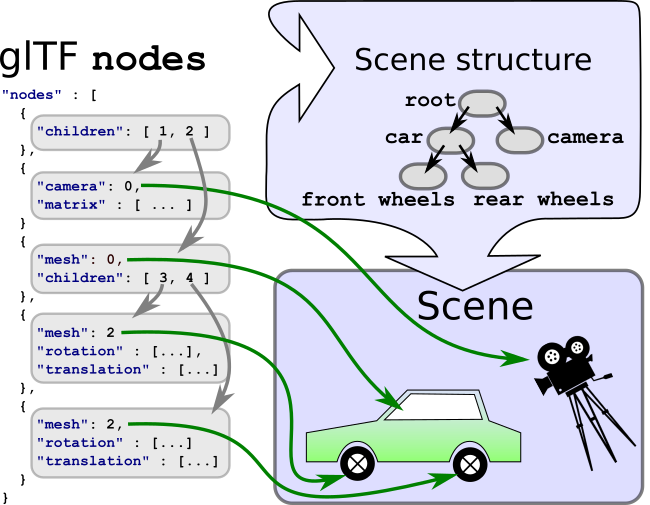
构成场景图的节点
每个node都可以包含一个名为 children数组,数组包含其子节点索引。因此,每个节点是节点层次结构的一个元素,它们一起将场景结构定义为场景图。
scene可以遍历在其中给出的每个节点,以递归方式访问其所有子节点,从而处理附加到节点的所有元素。此遍历的简化伪代码如下所示:
traverse(node) {
// Process the meshes, cameras, etc., that are
// attached to this node - discussed later
processElements(node);
// Recursively process all children
for each (child in node.children) {
traverse(child);
}
}
在实际中,将需要遍历一些附加信息:一些绑定到节点的元素的处理需要它们连到哪些节点的信息。另外,必须在遍历期间累积关于节点变换的信息。
本地和全局变换
每个节点都可以有一个变换。这种变换将定义平移、旋转或缩放。此转换将应用于节点本身及其所有子节点的所有元素。因此,节点的层次结构允许人们构造应用于场景元素的平移,旋转和缩放。
节点的局部变换
节点的局部变换可以有不同的表示。变换可以由matrix节点的属性直接给出。这是一个由16个浮点数组成的数组,以列主要顺序描述矩阵。例如,以下矩阵描述了关于(2,1,0.5)的缩放,围绕x轴旋转约30度,以及关于(10,20,30)的平移:
"node0": {
"matrix": [
2.0, 0.0, 0.0, 0.0,
0.0, 0.866, 0.5, 0.0,
0.0, -0.25, 0.433, 0.0,
10.0, 20.0, 30.0, 1.0
]
}
这里定义的矩阵如图4b所示
节点的变换也可以使用一个节点的translation, rotation, 和 scale属性给出,有时缩写为TRS:
"node0": {
"translation": [ 10.0, 20.0, 30.0 ],
"rotation": [ 0.259, 0.0, 0.0, 0.966 ],
"scale": [ 2.0, 1.0, 0.5 ]
}
这些属性中的每一个都可用于创建矩阵,然后这些矩阵的乘积是节点的局部变换:
- 该
translation只包含在x,y和z方向的平移。例如,从translation 中[ 10.0, 20.0, 30.0 ],可以创建将此translation 作为其最后一列的变换矩阵,如图4c所示。
rotation是作为四元数给出的。四元数的数学背景超出了本教程的范围。目前,最重要的信息是四元数是任意角度和任意轴旋转的简化表示。例如,四元数 [ 0.259, 0.0, 0.0, 0.966 ]描述围绕x轴旋转约30度。因此,此四元数可以转换为旋转矩阵,如图4d所示。
- scale给出沿x,y轴和z轴比例因子。可以通过使用这些缩放因子作为矩阵对角线上的条目来创建相应的矩阵。例如,缩放因子 [ 2.0, 1.0, 0.5 ] 的缩放矩阵如图4e所示。
当计算节点的最终局部变换矩阵时,这些矩阵被相乘。以正确的顺序执行这些矩阵的乘法非常重要。局部变换矩阵总是必须被计算为M = T * R * S,T即是平移矩阵translation, R即旋转矩阵rotation,S是比例矩阵scale。所以计算的伪代码是
translationMatrix = createTranslationMatrix(node.translation);
rotationMatrix = createRotationMatrix(node.rotation);
scaleMatrix = createScaleMatrix(node.scale);
localTransform = translationMatrix * rotationMatrix * scaleMatrix;
对于上面给出的示例矩阵,节点的最终局部变换矩阵如图4f所示。
该矩阵将根据赋予节点的scale,rotation和translation属性对格网的顶点进行缩放,然后旋转,最后平移。
当未给出三个属性中的任何一个时,将使用单位矩阵替换。类似地,当节点既不包含matrix属性也不包含TRS属性时,其局部变换将是单位矩阵。
节点的全局变换
无论JSON文件中的表示如何,节点的局部变换都可以存储为4×4矩阵。节点的全局变换由从根到相应节点的路径上的所有本地变换的乘积给出
Structure: local transform global transform
root R R
+- nodeA A R*A
+- nodeB B R*A*B
+- nodeC C R*A*C
重要的是要指出,在加载文件之后,这些全局变换不能只计算一次。稍后将展示动画如何修改各个节点的局部变换。这些修改将影响所有后续节点的全局变换。因此,当需要节点的全局变换时,必须直接从所有节点的当前局部变换计算它。或者,作为潜在的性能改进,实现可以缓存全局变换,检测祖先节点的局部变换中的变化,并且仅在必要时更新全局变换。对此的不同实现选项将取决于编程语言和客户端应用程序的要求,因此超出了本教程的范围。